A Machine Learning Guide for Econometricians – A Hands-on Approach
Abstract:
This paper attempts to present a hands-on guide for econometricians by providing practical examples along with a replicable R code. We first build an understanding of how the basic machine learning methods differ from the most widely used technique in the realm of econometrics and statistics and then provide two practical usages of these techniques. In the microeconomic example, we find that the Ridge regression outperforms the traditional Ordinary Least Squares Regression whereas the Elastic Net regression outperforms the most used model in the macroeconomic time-series forecasting, that is, the autoregressive model.
Keywords: OLS, Ridge, LASSO, EN, RMSE, Predictive, Forecasting
1. Introduction:
In the field of economic forecasting, two techniques stand as prominent pillars, the econometric models, and the machine learning (ML) models. Each of these techniques offer a variety of approaches and insights into understanding and forecasting economic indicators. For a long time econometric models have been the cornerstone of economic modelling with a primary focus on causal inference through rigorous statistical method such as the Ordinary Least Squares (OLS) regression [see Gujrati and Porter (2009) for details about the OLS regression]. However, with recent advanced in the field of ML a paradigm shift has occurred in forecasting techniques offering superior predictive performance and an ability to capture highly complex non-linear relationships, which is quite often an inherent property of economic data.
Econometrics mainly focuses on principles of classical statistics and make use of several estimation methods to model causal relationship between economic variables. Methods such as the OLS, instrumental variable estimation, vector autoregressive models, and many other estimation techniques are commonly employed to uncover the drivers of different economic phenomenon. Causal inference is mainly used to determine the role of different observable and unobservable economic indicators driving economic phenomenon such as consumption, investment, etc. or to evaluate policy interventions both at the micro and macro level.
In contract, ML techniques are mainly used for predictive modelling due to their superior prediction accuracy over causal inference. These methods make use of advanced algorithms to uncover patterns and relationships in the data, without imposition of strict assumptions about causality. By making use of large datasets and these complex yet powerful algorithms, ML models can capture highly non-linear patterns among the indicators of interest; thus, outperforming the traditional econometric techniques.
Many recent studies have shown ML model's ability to outperform the traditional econometric models. For instance, in the realm of macroeconomics, Medeiros et al. (2021) found the Least Absolute Shrinkage and Selection Operator (LASSO) and Random Forest (RF) techniques outperform econometric models in forecasting inflation in the United States (U.S.) economy. Syed et al. (2022) found that the ML outperforms fifteen econometric models in forecasting inflation in Pakistan. Similarly, in the context of microeconomics, Brahma and Mukherjee (2022) using a cross-sectional dataset find that the ML models, using area under the precision-recall curve, predicts incidences of neonatal and infant mortality in India better than the standard logistic regression. Chen and Ding (2023) performed academic performance prediction in schools across the state of Pennsylvania and found that the neural network (NN) outperformed the other ML models as well as the logistic regression in predicting academic performance.
Considering the above, this paper endeavors to provide a simple guide for econometricians providing them the basic understanding of several machine learning algorithms using a hands-on approach. To best of our knowledge it is the first paper that provides a detailed description of machine learning models for econometricians with practical examples from both macro and microeconomics. The structure of the paper is as follows. Section 2 introduces the basic econometric and ML models used for demonstration. Section 3 presents predictive analysis using a cross-sectional and time-series data along with replication code in R, which is an open-source programming language. Section 4 concludes.
2. The Econometric and Machine Learning Models:
This section contains details about the models used in our analysis. For microeconomics, we use the OLS as the base model for regression and put it in competition with the Ridge, the LASSO and the Elastic Net (EN) regressions. For Macroeconomics, we use the same ML models; however, we put them in competition with the AR model for comparison of forecast performance.
I. The Ordinary Least Squares:
The OLS is the most basic statistical technique that is employed widely to model the relationship between a dependent variable and one or more independent variables. The basic idea of the OLS is to find a set of regression coefficients for independent variables that minimize the sum of squared differences between the observed values of the target variable and the values predicted by the linear model. In our paper, we will resort to multiple linear regression than the simple linear regression that only contains a single explanatory variable. Mathematically, a multiple linear model can be written as:
The Ridge:
The Ridge regression is the first ML technique we apply in our analysis, motivated by Hoerl and Kennard (1970), the Ridge regression is a simple extension to the OLS model, where the authors in addition to minimizing the sum of squared residuals impose l_2-norm penalty term. Mathematically, the Ridge is written as:
The unique feature of the Ridge regression is its ability to address the issue of multi-collinearity and the issue of overfitting, which is commonly faced in OLS regression. It does it by lambda, which controls the shrinkage of the coefficients. Although, the Ridge squeezes the coefficients towards zero; however, they are never squeezed all the way to zero. This shrinkage allows reduction in variance of the estimated making them more stable and less sensitive to multi-collinearity. The size of the lambda is selected by the researcher, it is non-negative number. The higher the lambda, the stronger the regularization of the parameters, the more severe shrinkage of the larger coefficients.
The LASSO:
The LASSO is different from the Ridge and imposes a l_1-norm penalty term on top of minimizing the sum of squared residuals. It is mathematically written as:
LASSO is much more stringent in terms of avoidance of overfitting, and it not only squeezes the coefficients on the explanatory variables but also shrinks them all the way to zero. Thus, the variables whose coefficients are squeezed all the way to zero are dropped out of the regression. In this way the LASSO not only shrinks coefficients but also performs variable selection as well. This quality of LASSO has been termed as the sparsity-inducing effect. Like Ridge, the size of the lambda is selected by the researcher, it is non-negative number. The higher the lambda, the stronger the regularization of the parameters, the more severe shrinkage of the larger coefficients and a more likely elimination of a larger number of variables from the model.
Elastic Net:
EN which was proposed by Zou and Hastie (2005). It applies continuous shrinkage and variable selection simultaneously by employing penalized regression with both l_1 and l_2 penalty functions. Mathematically, it can be written as:
By applying both l_1 and l_2 penalty functions, EN obtains a superior ability to handle correlated predictors more effectively and to perform variable selection, while still maintaining benefits of regularization.
3. Predictive Analysis:
In this section we undertake predictive analysis using the cross-sectional micro data followed by time-series macroeconomic data. We use the methods explained above in both of these empirical exercises and attempt to determine if ML methods can outperform the econometric methods.
I. Microeconomic Predictive Analysis:
In this section, we conduct a predictive analysis using "Hitters" dataset from the library called "ISLR" in R. This dataset contains 20 variables for 263 baseball players.[2] We use 19 predictors from this dataset to predict the Salary of players. The dataset is first divided into a test and training dataset with a ratio of 70 and 30, respectively.[3] The lambda for choosing optimal penalty for the Ridge, the LASSO and EN is performed by 10-cross validation. The predictive performance is evaluated by the Root Mean Squared Errors (RMSE), Which is mathematically given by:
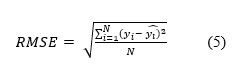
Where:
i is the variable i, N is the number of non-missing data points, y_i is the actual observations of the variable y, and (y_i ) ̂ is the predicted value of the target variable y. The code to replicate the results presented in Table 1 and 2 below is in Annexure I. Table 1 contains the optimal lambda used in our analysis for each of the ML techniques.
| Table 1: Optimal Value of the Lambda for ML techniques (Microeconomic Predictive Analysis) | |
| Name of the Machine Learning technique | Value of optimal lambda |
|---|---|
| Ridge | 30.70 |
| LASSO | 2.67 |
| Elastic Net | 1.92 |
Table 1 contains the optimal lambda for each of the ML models used in our study. It is evident from the table that Ridge has the highest lambda value of 30.70. In relative terms this value is quite high but it does not guarantee that the model will perform the best when it comes to the prediction of the variable of interest. To determine if it does perform well in predicting the salary of the baseball players. We report relative RMSEs in Table 2.
| Table 2: Relative RMSEs (Microeconomic Predictive Analysis) | |
| Name of the Machine Learning technique | Relative RMSE = RMSE ML / RMSE OLS |
|---|---|
| Ridge | 0.91 |
| LASSO | 0.95 |
| Elastic Net | 0.96 |
Table 1 shows that the Ridge model outperforms the OLS as well as the other ML techniques by producing a relative RMSE of 0.91 relative to the benchmark OLS model. This means that for the predictive exercise we are interested in this part of the paper, that is to predict the salary of the baseball players using 19 predictors, all the predictors are important as the Ridge regression do not drop any of the explanatory variables from the model.
II. Macroeconomic Forecasting Exercise:
In this section, we perform a forecasting exercise using a macroeconomic database. The database is called FRED-MD database, which contains data on macroeconomic variables for the economy of the United States (U.S.) McCracken and Ng (2016).[4] The dataset is transformed to made stationary as detailed in McCracken and Ng (2016) and in line with the vast literature the variables are standardized to have mean 0 and standard deviation 1 before we conduct the forecasting exercise.
We do not use the complete dataset comprising of data from January 1959 to January 2024 as it would have been computationally too much time-taking/costly. Instead, we cut the same into 20 years of data and drop all the variables that contain missing values. Hence, our sample extends from October 2003 to September 2023 (240 observations) for 99 variables. We forecast the Industrial Production growth for the U.S. economy in this simple illustration for understanding. Furthermore, we do not use rolling fixed window or rolling moving window forecast scheme instead we use the simple split the data into training dataset containing 228 observations and test dataset containing 12 months.[5]
Table 3 contains the value of optimal lambda for the Ridge, the LASSO and EN. These are computed using 10-fold cross validation method.
| Table 3: Optimal Value of the Lambda for ML techniques (Macroeconomic Forecasting Analysis) | |
| Name of the Machine Learning technique | Value of optimal lambda |
|---|---|
| Ridge | 0.100 |
| LASSO | 0.008 |
| Elastic Net | 0.007 |
Table 3 shows that the highest penalty for this dataset is also applied by the Ridge regression. However, if it also performs the best in forecasting the industrial production growth in the U.S. will only be clear once we estimate the model and compare its forecasting performance against the benchmark and other ML techniques.
The benchmark model for macroeconomic analysis is AR model of order 1 [AR(1)]. The autoregressive model is the regression model that regresses the variable of interest on the first lag of the variable itself. Mathematically, it can written as:
Where, y is the industrial production growth in our paper, α is the constant, β is the coefficient on the lagged industrial production growth, and ε_t is the white-noise error term. The results in terms of relative RMSE, that is, RMSE from ML techniques divided by the RMSE from the AR(1) model is reported in Table 4. Replication code for table 3 and 4 is available in Annexure II.
| Table 4: Relative RMSEs (Macroeconomic Forecasting Analysis) | |
| Name of the Machine Learning technique | Relative RMSE = RMSE ML/ RMSE AR(1) |
|---|---|
| Ridge | 0.15 |
| LASSO | 0.10 |
| Elastic Net | 0.09 |
Table 4 shows that the Elastic Net outperforms the benchmark as well as the other ML techniques in forecasting industrial production growth. It also shows that all the ML techniques were able to outperform the commonly used AR(1) model for forecasting macroeconomic variables. Although, the ML techniques are quite competitive among themselves; however, the EN stands out as the best for this macroeconomic forecasting exercise.
4. Conclusion:
This paper attempted to provide a hands-on exercise for both micro and macroeconomic forecasting analysis. We first explained in the simplest way the difference between the regularly used analysis for causal inference and in many a cases forecasting, that is the OLS and the sophisticated ML techniques such as the Ridge, the LASSO and EN.
We then performed a microeconomic analysis using a dataset containing information about 20 attributes for 263 baseball players. We found that the Ridge regression performed the best by beating forecast performance of the other ML techniques and the benchmark model, which is the best linear unbiased estimator, the OLS. Next, we performance a macroeconomic forecasting exercise using a large dataset for the U.S. economy. We forecasted the growth of industrial production for the U.S. and found that the EN outperformed all the ML techniques as well as the benchmark model, that is, AR(1).
The recent advances in computing has thus provided the econometricians and statisticians with the tools that can outperform the existing econometric models, especially in the area of forecasting, inline with the purpose of their creation.
References:
Brahma, D., & Mukherjee, D. (2022). Early warning signs: Targeting neonatal and infant mortality using machine learning. Applied Economics, 54(1), 57–74. https://doi.org/10.1080/00036846.2021.1958141
Chen, S., & Ding, Y. (2023). A Machine Learning Approach to Predicting Academic Performance in Pennsylvania's Schools. Social Sciences, 12(3), 118. https://doi.org/10.3390/socsci12030118
Gujarati, D. N., & Porter, D. C. (2009). Basic econometrics. McGraw-hill.
Hoerl, A. E., & Kennard, R. W. (1970). Ridge regression: Applications to nonorthogonal problems. Technometrics, 12(1), 69–82.
McCracken, M. W., & Ng, S. (2016). FRED-MD: A monthly database for macroeconomic research. Journal of Business & Economic Statistics, 34(4), 574–589.
Medeiros, M. C., Vasconcelos, G. F. R., Veiga, Á., & Zilberman, E. (2021). Forecasting Inflation in a Data-Rich Environment: The Benefits of Machine Learning Methods. Journal of Business & Economic Statistics, 39(1), 98–119. https://doi.org/10.1080/07350015.2019.1637745
Shah, S. A. A., Ishtiaq, M., Qureshi, S., & Fatima, K. (2022). Inflation Forecasting for Pakistan in a Data-rich Environment. The Pakistan Development Review, 61(4), 643–658.
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B: Statistical Methodology, 67(2), 301–320.
Annexures:
I. Code to replicate the Microeconomic Predictive Analysis Output:
library(ISLR) library(glmnet)
data(“Hitters”)
Hitters <- na.omit(Hitters)
Split data into training and testing sets (70:30 ratio)
set.seed(123) train_index <- sample(1:nrow(Hitters), round(0.7 * nrow(Hitters)))
train_data <- Hitters[train_index, ] test_data <- Hitters[-train_index, ]
Define predictors (features) and response variable
X_train <- as.matrix(train_data[, -which(names(train_data) == “Salary”)]) y_train <- train_data$Salary
X_test <- as.matrix(test_data[, -which(names(test_data) == “Salary”)]) y_test <- test_data$Salary
ols_model <- lm(Salary ~ ., data = train_data)
Perform 10-fold cross-validation to choose lambda for Ridge regression
ridge_cv <- cv.glmnet(X_train, y_train, alpha = 0, nfolds = 10)
Perform 10-fold cross-validation to choose lambda for Lasso regression
lasso_cv <- cv.glmnet(X_train, y_train, alpha = 1, nfolds = 10)
Perform 10-fold cross-validation to choose lambda for Elastic Net regression
elastic_net_cv <- cv.glmnet(X_train, y_train, alpha = 0.5, nfolds = 10)
optimal_lambda_ridge <- ridge_cv![]() lambda.min
optimal_lambda_elastic_net <- elastic_net_cv$lambda.min
lambda.min
optimal_lambda_elastic_net <- elastic_net_cv$lambda.min
# Create a dataframe with names of techniques and their optimal lambda values
lambda_values_df <- data.frame(Technique = c("Ridge", "Lasso", "Elastic Net"),
Optimal_Lambda = c(ridge_cv$lambda.min,
lasso_cv$lambda.min,
elastic_net_cv$lambda.min))
Print the dataframe
print(lambda_values_df)
Fit Ridge regression model with optimal lambda
ridge_model <- glmnet(X_train, y_train, alpha = 0, lambda = optimal_lambda_ridge)
Fit Lasso regression model with optimal lambda
lasso_model <- glmnet(X_train, y_train, alpha = 1, lambda = optimal_lambda_lasso)
Fit Elastic Net regression model with optimal lambda
elastic_net_model <- glmnet(X_train, y_train, alpha = 0.5, lambda = optimal_lambda_elastic_net)
ols_preds <- predict(ols_model, newdata = test_data) ridge_preds <- predict(ridge_model, newx = X_test) lasso_preds <- predict(lasso_model, newx = X_test) elastic_net_preds <- predict(elastic_net_model, newx = X_test)
rmse_ols <- sqrt(mean((ols_preds - test_data$Salary)^2)) rmse_ridge <- sqrt(mean((ridge_preds - y_test)^2)) rmse_lasso <- sqrt(mean((lasso_preds - y_test)^2)) rmse_elastic_net <- sqrt(mean((elastic_net_preds - y_test)^2))
cat(“RMSE - OLS Regression:”, rmse_ols, “”) cat(“RMSE - Ridge Regression:”, rmse_ridge, “”) cat(“RMSE - Lasso Regression:”, rmse_lasso, “”) cat(“RMSE - Elastic Net Regression:”, rmse_elastic_net, “”)
Compute Relative RMSEs - Relative RMSE = RMSE ML / RMSE OLS
relative_rmse_ridge <- rmse_ridge / rmse_ols relative_rmse_lasso <- rmse_lasso / rmse_ols relative_rmse_elastic_net <- rmse_elastic_net / rmse_ols
Create a matrix of relative RMSEs
relative_rmse_matrix <- matrix(c(relative_rmse_ridge, relative_rmse_lasso, relative_rmse_elastic_net), nrow = 1, byrow = TRUE, dimnames = list(NULL, c(“Ridge”, “Lasso”, “Elastic Net”)))
Print relative RMSE matrix
print(relative_rmse_matrix)
II. Code to replicate the Microeconomic Predictive Analysis Output:
library(glmnet) library(Metrics) library(BVAR) library(ModelMetrics)
help(package = “BVAR”)
fredmd <- fred_md
Identify columns with missing values
missing_cols <- colnames(fredmd)[colSums(is.na(fredmd)) > 0]
Drop columns with missing values
fredmd_clean <- fredmd[, !colnames(fredmd) %in% missing_cols]
Print the names of dropped variables
print(missing_cols)
Building a final transformed dataset for forecasting
fredmd_f <- fred_transform(fredmd_clean, type = c(“fred_md”),,,lag = 1, scale = 100)
Scaling the variables in line with the standard literature on forecasting
fredmd_s <- data.frame(scale(fredmd_f, center = T, scale = T))
Making a 10 year dataset for Illustration
fredmd_s_ar <- fredmd_s[536:775,c(5,60,82)]
Define the length of training data
train_length <- 228
train_data <- INDPRO[1:train_length]
ar_model <- arima(train_data, order = c(1, 0, 0))
forecast_values <- predict(ar_model, n.ahead = 12)$pred
Extract the actual values for next 12 periods
actual_values <- INDPRO[(train_length + 1):(train_length + 12)]
rmse <- sqrt(mean((actual_values - forecast_values)^2))
print(rmse)
set.seed(157)
Dataframe is named as fremd_s, Extract target variable and regressors
target_variable <- fredmd_s[, 5] regressors <- fredmd_s[, -5] # Exclude the target variable
Split the data into training and test sets
train_indices <- 1:228 test_indices <- 229:240
test_target <- target_variable[test_indices] test_regressors <- regressors[test_indices, ]
Ridge regression with 10-fold cross-validation
ridge_model <- cv.glmnet(x = as.matrix(train_regressors), y = train_target, alpha = 0, nfolds = 10) optimal_lambda_ridge <- ridge_model$lambda.min ridge_pred <- predict(ridge_model, s = optimal_lambda_ridge, newx = as.matrix(test_regressors)) ridge_rmse <- rmse(test_target, ridge_pred)
LASSO regression with 10-fold cross-validation
lasso_model <- cv.glmnet(x = as.matrix(train_regressors), y = train_target, alpha = 1, nfolds = 10) optimal_lambda_lasso <- lasso_model$lambda.min lasso_pred <- predict(lasso_model, s = optimal_lambda_lasso, newx = as.matrix(test_regressors)) lasso_rmse <- rmse(test_target, lasso_pred)
Elastic Net regression with 10-fold cross-validation
elastic_net_model <- cv.glmnet(x = as.matrix(train_regressors), y = train_target, alpha = 0.5, nfolds = 10) optimal_lambda_elastic_net <- elastic_net_model$lambda.min elastic_net_pred <- predict(elastic_net_model, s = optimal_lambda_elastic_net, newx = as.matrix(test_regressors)) elastic_net_rmse <- rmse(test_target, elastic_net_pred)
print(c(optimal_lambda_ridge, optimal_lambda_lasso, optimal_lambda_elastic_net))
Print Relative RMSE values
relative_rmse_ip <- (c(ridge_rmse, lasso_rmse, elastic_net_rmse)/rmse) print(relative_rmse_ip)
EGF Blogs
© Institute of Business Administration (IBA) Karachi. All Rights Reserved.